Reinforcement Learning 進階篇:Deep Q-Learning
繼上一篇Reinforcement Learning 健身房:OpenAI Gym 介紹以 Q-table 為基礎的 Q-learning 之後,這一篇要來結合 PyTorch 實現以深度學習為基礎的 Deep Q-Learning。
* 請注意,以下只針對Python3進行講解與測試,並以 MacOSX 為環境。讀者應具備基礎 neural network 及 reinforcement learning 知識,可先閱讀 PyTorch 介紹 及 Reinforcement Learning 介紹。
在上一篇的實作中,運用 Q-table 可以成功的讓 agent 學習到如何維持小車上柱子的平衡。但是 Q-table 並不能有效解決所有問題,為什麼呢?此篇將從 Q-table 的侷限講起,帶入 Deep Q-Learning 的原理及為何它能突破限制,最後講解參考自莫凡Python的 Deep Q-Learning 實作。文末獻醜一下自己做的(很弱沒成功的)用 reinforcement learning 解密碼的小專案,期待有人能成功訓練出一個解碼器。
Deep Q-Learning 原理
在 Q-table 的實作中,我們知道整個 Q-table 就是一個以 state 和 action 為索引儲存 Q value 的表格。不過在 state 和 action 有限且不過多的情況下,這個索引表格才有可能被建立,例如 CartPole 問題中 state 只有四個 feature,每個的值都在有限範圍內(或是可以固定在有限範圍),action 更只有兩個值。
但如果今天我們的 state 來自遊戲畫面,或圍棋棋盤呢?你可以選擇根據任務原理,很辛苦又可能徒勞無功的把環境簡化成幾個有效的 feature 當作 state;或是選擇用 deep neural network 幫我們提取 feature 並逼近我們要的 Q function,亦即今天要介紹的 Deep Q-Learning。
對 neural network 有概念的話應該不難看出 deep Q-learning 的理念。所謂 neural network 就是藉由不斷被餵食 input-output pair 後,最終逼近 input-output 對應關係的 function,亦即 f(input) = output。把它轉成 policy π(state) = action 的形式,是不是就能看出為什麼學者會想把它塞進 Reinforcement Learning 裡了呢?
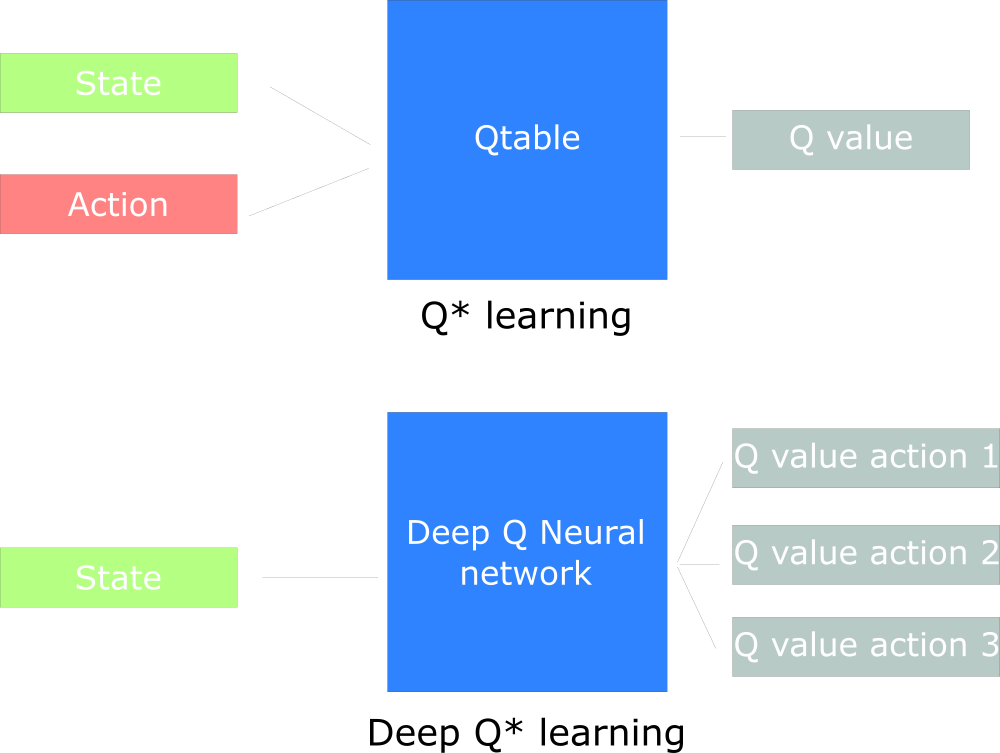
由 neural network 取代 Q-table 的好處是,neural network 可以搭配不同變形,從龐大的 state space 中自動提取特徵,例如經典的 Playing Atari with Deep Reinforcement Learning 即是以 Convolutional Neural Network 直接以遊戲畫面的 raw pixel 下去訓練;這是僵化的 Q-table 辦不到的。
Deep Q-Learning 實作
GitHub 完整程式碼:https://github.com/pyliaorachel/openai-gym-cartpole;原始碼修改自這篇文章,有87成像。
同樣以 CartPole 為範例,用 PyTorch 打造 Deep Q-Network 來實作 Deep Q-Learning。以下總共有三步驟,不過在開始前,要先介紹一些小技巧來增進訓練穩定性。
Deep Q-Network 穩定小技巧
在 Human-level control through deep reinforcement learning 這篇論文裡,為 Deep Q-Learning 的訓練穩定性提供了三項解藥:
- Use experience replay,亦即把 experience 存在 memory 中,訓練時隨機從中抽樣。這麼做可以打亂這些 experience 之間沒有必要的時間關係。
- Freeze target Q-network,即建立兩種 Q-network,一為實際進行訓練的 evaluation network,一為訓練目標 target network,其中 target network 久久更新一次,更新時直接把 evaluation network 的參數整組複製過來。還記得 Q function 的遞迴關係:
Q(s, a) = r + γ * max_a' Q(s', a')嗎?如果只訓練一個 network,則每更新一次,不只是正在訓練的Q(s, a)在變,我們的目標Q(s', a')也跟著在變!整個 network 會像是自己追著自己的尾巴一樣,無法趨於穩定。 - Clip rewards,即限縮 reward 的值,以利 backpropagation 中能有穩定的 gradient 計算。
這些小技巧將會融入我們的實作中。
Step 1: 建立 Network
首先建立一層 hidden layer 的 neural network,把 state 傳入後,得出每個 action 的分數,分數越高的 action 越有機會被挑選。而我們的目標是在當前 state 下,讓對未來越有利的 action 分數能越高。
class Net(nn.Module):
def __init__(self, n_states, n_actions, n_hidden):
super(Net, self).__init__()
# 輸入層 (state) 到隱藏層,隱藏層到輸出層 (action)
self.fc1 = nn.Linear(n_states, n_hidden)
self.out = nn.Linear(n_hidden, n_actions)
def forward(self, x):
x = self.fc1(x)
x = F.relu(x) # ReLU activation
actions_value = self.out(x)
return actions_value
Step 2: 建立 Deep Q-Network
在小技巧中提到,總共需要兩個 network,evaluation network (eval_net) 及 target network (target_net)。除此之外,還要有 memory 儲存 experience,以及設定好參數:
class DQN(object):
def __init__(self, n_states, n_actions, n_hidden, batch_size, lr, epsilon, gamma, target_replace_iter, memory_capacity):
self.eval_net, self.target_net = Net(n_states, n_actions, n_hidden), Net(n_states, n_actions, n_hidden)
self.memory = np.zeros((memory_capacity, n_states * 2 + 2)) # 每個 memory 中的 experience 大小為 (state + next state + reward + action)
self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=lr)
self.loss_func = nn.MSELoss()
self.memory_counter = 0
self.learn_step_counter = 0 # 讓 target network 知道什麼時候要更新
self.n_states = n_states
self.n_actions = n_actions
self.n_hidden = n_hidden
self.batch_size = batch_size
self.lr = lr
self.epsilon = epsilon
self.gamma = gamma
self.target_replace_iter = target_replace_iter
self.memory_capacity = memory_capacity
def choose_action(self):
pass
def store_transition(self):
pass
def learn(self):
pass
choose_action 會根據 epsilon-greedy policy 選擇 action。上次有提到,epsilon 表機率,訓練過程中有 epsilon 的機率 agent 會選擇亂(隨機)走,如此才有機會學習到新經驗:
def choose_action(self, state):
x = torch.unsqueeze(torch.FloatTensor(state), 0)
# epsilon-greedy
if np.random.uniform() < self.epsilon: # 隨機
action = np.random.randint(0, self.n_actions)
else: # 根據現有 policy 做最好的選擇
actions_value = self.eval_net(x) # 以現有 eval net 得出各個 action 的分數
action = torch.max(actions_value, 1)[1].data.numpy()[0] # 挑選最高分的 action
return action
再來 DQN 需要儲存 experience:
def store_transition(self, state, action, reward, next_state):
# 打包 experience
transition = np.hstack((state, [action, reward], next_state))
# 存進 memory;舊 memory 可能會被覆蓋
index = self.memory_counter % self.memory_capacity
self.memory[index, :] = transition
self.memory_counter += 1
最後是從 memory 中取樣學習:
def learn(self):
# 隨機取樣 batch_size 個 experience
sample_index = np.random.choice(self.memory_capacity, self.batch_size)
b_memory = self.memory[sample_index, :]
b_state = torch.FloatTensor(b_memory[:, :self.n_states])
b_action = torch.LongTensor(b_memory[:, self.n_states:self.n_states+1].astype(int))
b_reward = torch.FloatTensor(b_memory[:, self.n_states+1:self.n_states+2])
b_next_state = torch.FloatTensor(b_memory[:, -self.n_states:])
# 計算現有 eval net 和 target net 得出 Q value 的落差
q_eval = self.eval_net(b_state).gather(1, b_action) # 重新計算這些 experience 當下 eval net 所得出的 Q value
q_next = self.target_net(b_next_state).detach() # detach 才不會訓練到 target net
q_target = b_reward + self.gamma * q_next.max(1)[0].view(self.batch_size, 1) # 計算這些 experience 當下 target net 所得出的 Q value
loss = self.loss_func(q_eval, q_target)
# Backpropagation
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
# 每隔一段時間 (target_replace_iter), 更新 target net,即複製 eval net 到 target net
self.learn_step_counter += 1
if self.learn_step_counter % self.target_replace_iter == 0:
self.target_net.load_state_dict(self.eval_net.state_dict())
Step 3: 訓練
訓練過程是 1. 選擇 action 2. 儲存 experience 3. 訓練:
env = gym.make('CartPole-v0')
# Environment parameters
n_actions = env.action_space.n
n_states = env.observation_space.shape[0]
# Hyper parameters
n_hidden = 50
batch_size = 32
lr = 0.01 # learning rate
epsilon = 0.1 # epsilon-greedy
gamma = 0.9 # reward discount factor
target_replace_iter = 100 # target network 更新間隔
memory_capacity = 2000
n_episodes = 4000
# 建立 DQN
dqn = DQN(n_states, n_actions, n_hidden, batch_size, lr, epsilon, gamma, target_replace_iter, memory_capacity)
# 學習
for i_episode in range(n_episodes):
t = 0
rewards = 0
state = env.reset()
while True:
env.render()
# 選擇 action
action = dqn.choose_action(state)
next_state, reward, done, info = env.step(action)
# 儲存 experience
dqn.store_transition(state, action, reward, next_state)
# 累積 reward
rewards += reward
# 有足夠 experience 後進行訓練
if dqn.memory_counter > memory_capacity:
dqn.learn()
# 進入下一 state
state = next_state
if done:
print('Episode finished after {} timesteps, total rewards {}'.format(t+1, rewards))
break
t += 1
env.close()
結果
訓練最後幾步的結果如下:

什麼?也太糟了吧。整個訓練看不出有收斂,至少跑了 4000 個 episode 的情況下是如此。
讓我們重新看看 reward 是怎麼獲得的。一切都在 gym 給的 environment 裡:
...
if not done:
reward = 1.0
elif self.steps_beyond_done is None:
# Pole just fell!
self.steps_beyond_done = 0
reward = 1.0
else:
self.steps_beyond_done += 1
reward = 0.0
...
也就是柱子倒了之後獲得 0 分,其他情況下獲得 1 分。這麼缺乏資訊的 reward,得有勞 agent 嘗試好幾回才能學會怎麼維持柱子平衡。
讓我們稍微作弊一下,自己建立 reward 分配方法,讓 reward 提供更多資訊。很直覺的,柱子的角度越正,reward 應該越大。另外若想要小車保持在中間,那麼小車跟中間的距離越小,reward 也應該越大:
...
next_state, reward, done, info = env.step(action)
# 修改 reward,加快訓練
x, v, theta, omega = next_state
r1 = (env.x_threshold - abs(x)) / env.x_threshold - 0.8 # 小車離中間越近越好
r2 = (env.theta_threshold_radians - abs(theta)) / env.theta_threshold_radians - 0.5 # 柱子越正越好
reward = r1 + r2
dqn.store_transition(state, action, reward, next_state)
...
把 episode 調到 400 次,已經能有不錯的訓練結果了:

這邊注意不能直接拿 reward 的值相比,因為方法不同,主要是看 timestep,就是柱子維持不倒的時間。如果自己跑跑看,可以看到柱子在訓練後期可以穩定站立在小車上。
不重要小獻醜:Reinforcement Learning 解碼器
GitHub 完整程式碼:https://github.com/pyliaorachel/reinforcement-learning-decipher
之前的課堂作業裡,我選擇嘗試 reinforcement learning 來解凱薩密碼,就是一種很簡單的替換加密技術。難點在於,希望用 RNN 捕捉 state 和 state 之間的時間關係,以及學會密碼的偏移量。
結果其實很不理想,連長度 2~4 的密碼都解不開,最後因為時間關係就馬馬虎虎的交了(分數還挺高的就是)。我有寫一份 report,有興趣可以看看,還算有一些小成果。專案裡也有我設置的解密環境,有興趣可以載來玩玩,看看能不能幫我改善演算法。
結語
本篇介紹了最基本的 Deep Q-Learning 原理及實作,雖然可以克服 Q-table 的容量限制,但訓練難度增加不少,包括訓練穩定性及速度等等,都要費時調教一番,有時還需要引進旁門左道...我是說,小撇步,來增加訓練效率。其實 Deep Reinforcement Learning 還有很多進化之作,就待有興趣的讀者自行深入探討了。
參考資料
- DQN 强化学习
- An introduction to Deep Q-Learning: let’s play Doom
- PowerPoint: Human-Level Control through Deep Reinforcement Learning